Desde hace algún tiempo estoy haciendo un proyectillo por mi cuenta de comparación de software en base a su comportamiento y a la estructura del binario. Para el análisis de la estructura del ejecutable obtengo datos de las funciones que componen el programa, sus conexiones con otras funciones, número de bloques básicos de cada función y otros datos estadísticos sacados a partir de estos conceptos.

Con esos datos de como se interrelacionan las funciones de un programa entre sí obtengo el «callgraph» del programa (un grafo dirigido de las relaciones de las funciones del programa entre si). En el ejemplo siguiente podéis ver el callgraph de un programa bastante simple sacado con el IDA:

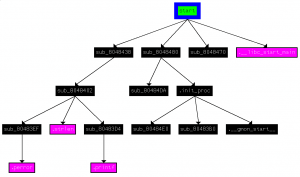
En este gráfico se puede observar como se llama desde el punto de entrada a cada una de las funciones del programa y que funciones llaman a cuales.

Para sacar estos datos utilizo IDA Pro y unos cuantos scripts en IDA Python ya que, de otro modo, hacer todo lo que ya hace mágicamente IDA sería, además, de todo un proyecto por su propia cuenta, un suplicio (y no tengo ganas de meterme aún en más berenjenales). Para realizar las comparaciones, simplemente, uso datos estadísticos de la complejidad ciclomática, número de funciones con interacción con otras funciones del programa y poco más (quería algo simple y que funcionara en un porcentaje de casos alto, no necesariamente en todos).

Bueno, hasta aquí todo iba bien y el mundo era feliz. Pero, de repente, me surgió un problema muy grande y muy gordo. Imaginemos que una parte grande de código es compartida entre 2 programas que poco o nada tienen que ver entre sí. Nosotros queremos obtener esa parte de código compartido entre ambos programas. Por poner el ejemplo más claro, imaginemos 2 binarios que han sido infectados por un mismo virus: Ambos programas (que no tienen porque tener nada en común entre si) comparten un mismo código viral. Pues este es el gran problema: ¿Cómo puedo obtener ese código específico del virus comparando los grafos de los 2 programas infectados? Y entonces empezaron los días no tan felices.

El problema en cuestión es conocido como “Maximun Common Subgraph Isomorphism Problem”. La primera idea que me vino a la mente es crear la matriz de adyacencia de ambos callgraphs y compararlas. Para quienes no sepáis que son las matrices de adyacencia os dejo la definición que da la Wikipedia:

“La matriz de adyacencia es una matriz cuadrada que se utiliza como una forma de representar relaciones binarias.”

La verdad es que la explicación formal de que es una matriz de adyacencia dada por la Wikipedia, será muy buena, pero no aclara mucho así que lo mejor es ver un simple ejemplo.

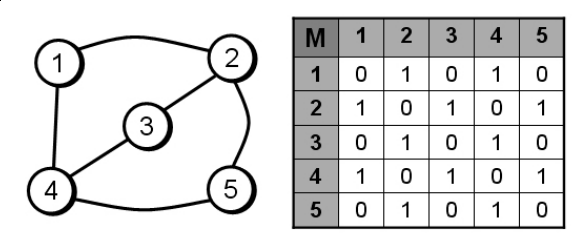
En esta imagen vemos un grafo (izquierda) y su matriz de adyacencia (derecha). El nodo 1, se relaciona con el nodo 2 y el nodo 4, así pues, en la matriz de adyacencia, marcamos con un “1” aquellos puntos con los que se relaciona. Después de hacer lo mismo con todos los nodos ya tenemos la matriz de adyacencia.

Explicado este tema, ahora viene cuando la mataron. Como comentaba un poco más arriba, mi primera idea fue utilizar la matriz de adyacencia del callgraph de los 2 programas a comparar para buscar un subgrafo. Para ello cogía el grafo más pequeño y lo superponía en cada una de las posiciones del grafo más grande contando el número de aciertos (unos y ceros que coincidían) y guardándome el conjunto con mayor número de aciertos. Claro, esto es de todo menos rápido. Además había otro problema aún más gordo: ¿Los callgraph de un programa normal y corriente son tan diminutos como los ejemplos que he puesto aquí? Ni de lejos. Un programa simple puede tener miles de funciones y, almacenar en memoria matrices de adyacencia de, por ejemplo, 2048×2048 elementos y compararlas es una p* burrada.

Así que nada, tenía que buscar otra solución y aquí es donde me quedé estancado una buena temporada (también porque otros temas de la “vida cotidiana” me recortaron bastante tiempo y tal…). Estuve mareando a la gente de 48bits buscando ideas y buscando por internet cuales eran los algoritmos más utilizados para este tipo de problemáticas ya que, por supuesto, alguien anteriormente se había planteado el mismo problema que yo y lo había resuelto. Lo que más encontraba eran referencias al Algoritmo de Ullman para búsqueda de subestructuras (que parece ser que es el algoritmo de búsqueda de subestructuras más utilizado en la industria química) que utilizaba matrices de adyacencia, que es precisamente, lo que quería evitar. Así que no me valía tampoco…

El caso es que, Inocram y Ruben me dieron una muy buena idea: ¿Y no lo puedes pasar a algo parecido a una cadena para poder hacer el LCS (Longest Common Subsequence) de la misma? El primer impulso (idea también de Ruben) fue coger la matriz de adyacencia otra vez y escribir toda la ristra de unos y ceros seguida e intentar compararla con otra ristra de unos y ceros seguidos de otra matriz de adyacencia, osea, del segundo programa a comparar. Nada, no valía. Si la matriz de adyacencia no tiene el mismo número de elementos, lo que encuentre (si encuentra algo) no vale.

Seguí buscando otros métodos de poder representar un grafo dirigido como una cadena y me encontré un artículo en el que mostraban como con ciertos algoritmos sacaban fingerprints de ciertas estructuras moleculares, en algunos casos incluso usando software libre:

http://depth-first.com/articles/2008/10/03/fast-substructure-search-using-open-source-tools-part-2-fingerprint-screen-with-sql

Con las ideas de la peña de 48bits y con lo que encontraba en la internete llegué a la conclusión de que tenía que buscar un medio de hacer un fingerprint de la estructura del grafo que, además, no tenía que ser tan brutalmente grande como la matriz de adyacencia. Y entonces llegué a las listas de adyacencia.

Las listas de adyacencia no son sino, simplemente, unas listas en las que se indican solamente que nodos se relacionan con otros nodos (en las matrices de adyacencia se guarda la información total, tanto de los nodos que tienen relación entre sí, como los que no). La lista de adyacencia del siguiente gráfico:

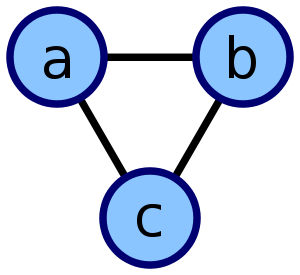
…sería la siguiente:

{a,b}, {a,c}, {b,c}

Pero nuevamente surgen problemas. ¿Cómo puedo comparar 2 listas de adyacencia? Pues simplemente, al menos con la representación que se le da, parece que no se puede. Más que otra cosa, porque con la lista de adyacencia se pierde información de los nodos, es decir, no sabemos identificar exactamente los nodos cuando queremos comparar 2 listas de adyacencia. Otra vez lo mismo de antes, tengo que buscar otra solución…

Buscando otra vez más por internet, y después de guarretear un cuaderno entero con “pelotitas” y “rallitas” como me decía un amigo (y viendo las caras de mi novia preguntándose a sí misma si estaba segura de querer continuar la relación conmigo y tal…), me encontré una presentación de Ero Carrera de VxClass en la que comentaban que como fingerprint de una función (entre otras varias cosas), utilizaban el grado de entrada (número de funciones que llaman a dicha función), el grado de salida (número de funciones a las que llama una función) y su complejidad ciclomática (que no la uso en mi ejemplo). Y así encontré una posible solución: Representar el grafo como una lista en la que solamente almaceno el “indegree” y “outdegree”. Por ejemplo, dado el siguiente grafo:

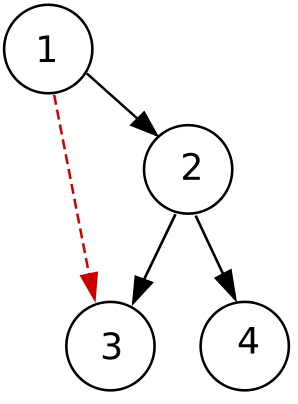
La lista que obtendría sería la siguiente:

{0,2}, {2,0}, {1,2}, {1,0}

Donde, el primer par {0,2}, indicaría que el primer nodo tiene grado cero de entrada, y grado 2 de salida (vamos, que no tiene ninguna conexión de nivel y superior y que desde ese nodo se llama a otros 2 nodos diferentes), el segundo par {2,0}, tiene 2 nodos de entrada y 0 de salida y así sucesivamente.

Y así he encontrado un medio (que más o menos funciona) de como sacar subgrafos comunes a partir de 2 grafos (o como sacar el subgrafo isomorfo más grande común entre 2 grafos).

Os pongo un pequeño código de ejemplo en Python de implementación de toda esta movida (el código es de todo menos óptimo, pero solo es un ejemplo):

En la función «test2» se cogen las listas creadas como cuento yo 2 de 2 grafos que me los he inventado y se obtiene el subgrafo isomorfo a ambos. En el ejemplo «test3», a partir de una matriz de adyacencia, se obtiene la lista creada como cuento en el post este y se saca también el subgrafo isomorfo a los 2 grafos.

Sea como sea, esto tiene varios problemas. Entre los que me he encontrado, por ejemplo, el primero de todos (y más importante, creo yo) es que puede encontrarse un subgrafo isomorfo por casualidad con estos datos y que, realmente, no valga 🙁 Pero bueno, es un modo de aproximarse (se podría verificar a posteriori si ese isomorfismo sacado es correcto o no utilizando otros algoritmos que aunque sean más pesados solo se aplicarían en caso de haber pasado el primer filtro). El otro problema que encuentro es que, el primer nodo y el último que deberían de marcar el isomorfismo, no tienen porque tener el mismo «indegree» y «outdegree». De hecho, el primer nodo puede llegar a tener un indegree mayor o igual que en el subgrafo real comparado con el extraído de ambos grafos a comparar y, el último nodo, tener un outdegree mayor o igual. Pero bueno, funciona en un porcentaje de casos bastante alto según mis pruebas y algo es algo.

Pues bueno, eso es todo. Ya sé que tampoco no es nada del otro mundo, pero es un problema que a mí me ha traído de cabeza durante algún tiempo y que me ha parecido bonito de contar. Espero que no haya sido mucha chapa tampoco todo el texto.

DISCLAIMER: Yo no tengo ni zorra idea de matemáticas y lo que pongo aquí es lo que he ido aprendiendo por mi cuenta así que puede que haya cosas que no estén «muy finas» y que mis «definiciones formales» sean una puta mierda.