Buenas tardes a todos y todas!

Hace poco estuve resolviendo algunos de los problemas propuestos en el Code Jam, el concurso deprogramacion organizado por Google. Este concurso me parece interesante porque los problemas que hay que resolver difieren bastante del tipo de problemas a los que estoy acostumbrado a enfrentarme en mi trabajo diario. Hoy voy a comentaros el analisis que hice, y que a la postre me llevo hasta la solucion, de uno de esos problemas.

Tengo que confesar que aunque me he divertido la falta de practica y de habilidad me han dificultado enormemente la tarea. Es probable que para muchos de los que lean esto los argumentos y deducciones les parezcan triviales, y la solucion evidente.

Sin mas dilacion, voy a pasar a explicar brevemente el problema propuesto. Imaginaros un edificio con un numero indeterminado de plantas. Si desde una planta de ese edificio lanzamos un huevo y este se rompe, entonces el huevo tambien se rompe al lanzarlo desde cualquiera de las plantas que se encuentran por encima. Si el huevo no se rompe, entonces tampoco se rompe al lanzarlo desde cualquiera de las plantas que se encuentran por debajo. Ahora imaginaros que disponemos de H huevos de los cuales solo podemos romper B. Lo que tenemos que hacer es calcular el numero maximo de plantas para las que siempre somos capaces de encontrar la planta a partir de la cual los huevos, al ser lanzados por la ventana, comienzan a romperse.

Hay dos aspectos de este problema que son evidentes. Si solo podemos romper un huevo, entonces el numero maximo de plantas del edificio sera igual al numero de huevos del que disponemos. Esto es asi porque nuestra unica posibilidad es ir probando las plantas una a una:

Por otro lado, si podemos romper todos los huevos entonces la mejor solución es ir haciendo una busqueda dicotomica en el edificio, de forma que el numero maximo de planta seria:

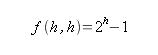
Una vez que tenemos los casos base fijados, es facil definir una funcion recursiva que solucione el problema. Cuando tiramos un huevo desde una de las plantas, dicho huevo puede romperse o no romperse. Dependiendo del resultado, dispondremos de un huevo menos (Cuando el huevo no se rompe), o dispondremos de un huevo menos y podremos romper un huevo menos (Cuando el huevo se rompe). La suma de las posibilidades de estos dos conjuntos mas la planta desde la que hemos probado nos da el numero maximo de plantas que estamos buscando:

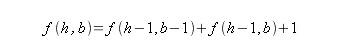
Es evidente que la implementacion de esa funcion recursiva es un suicidio computacional. Las diferentes llamadas recursivas comenzarian a calcular muchisimas veces los mismos valores perdiendo una gran cantidad de tiempo. Para evitar este problema disponemos de la programacion dinamica. El problema de las funciones recursivas de este tipo es que tienden a calcular varias veces los mismos datos. Dicho de otra forma, que en el proceso de recursion los subproblemas se repiten. Precisamente es la existencia de estos problemas superpuestos lo que trata de usar la programacion dinamica para acelerar la resolucion del problema. Si analizamos la formula anterior podemos ver que sabiendo las posibilidades de las que disponemos para n-1 huevos, podemos calcular cualquier posibilidad para n huevos. Si comenzamos calculando las posibilidades para f(1,1) podremos calcular todas las posibilidades para f(2,x), desde ahi podremos calcular las posibilidades para f(3,x) y así sucesivamente. De esta forma optimizaremos el calculo de los subproblemas. De esta forma podriamos construir un triangulo, en el que las columnas representan el numero de huevos que podemos romper, y las filas el numero de huevos del que disponemos:

Para nuestra implementacion solo necesitamos almacenar los datos de la fila anterior a la que estamos calculando, por lo que un array de B posiciones es suficiente para almacenar los datos:

Esta solucion es bastante buena. Hay que tener en cuenta que cuando podemos romper mas de 33 huevos necesitamos mas de 32 bits para almacenar el numero de planta del edificio. Un control para evitar los Overflows tambien limitaria el tiempo del calculo obteniendo un buen rendimiento. Pero de todas formas el coste cuadratico del algoritmo no me enrolla mucho, asi que es el momento de buscar algo mejor. Para ello nos debemos adentrar, como es costumbre, en el mundo de las ideas felices.

Si nos fijamos en la funcion recursiva que hemos descrito al principio, podemos ver que se asemeja bastante a la identidad de Pascal:

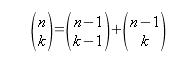
Hay otro dato curioso y que tambien me hace sospechar, y se refiere a otra identidad bien conocido. El numero total de los subconjuntos de un conjunto se puede definir de la siguiente manera (Los coeficientes binomiales tambien represetan el numero de subconjuntos de k elementos que se pueden construir a partir de un conjunto de n elementos):

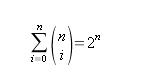
El numero de subconjuntos de un conjunto parece relacionarse con f(n,n). Por lo tanto, parece que hay alguna relacion entre los coeficientes binomiales y los datos que nosotros estamos calculando. Teniendo en cuenta los datos expuestos arriba parece que practicamente se puede establacer una relacion entre los coeficiontes binomiales y nuestra funcion f. Ahora viene el dato definitivo. Si en el triangulo que hemos contruido antes, restamos a cada columna la columna que tiene a su izquierda, lo que obtenemos es:

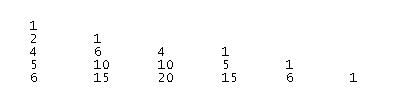
Que resulta ser el triangulo de Pascal! A excepcion de que las lineas no comienzan con 1… Ese 1 que falta es el dato del calculo de «N sobre 0», que representa al conjunto vacio, subconjunto de todos los conjuntos. El trianguno de Pascal representa los coeficientes binomiales, por lo que ahora podemos definir nuestra funcion f como:

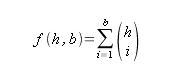
Y teniendo en cuenta que la definicion de «n sobre k» en base al factorial es de la siguiente forma:

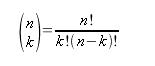
con todos estos datos ya hemos sentado las bases para una implementacion bastante mas optima que la anterior, puesto que ahora estamos en posicion de implementar un algoritmo lineal ( O(B) ) y con un consumo de memoria constante:

Espero que hayais disfrutado de la lectura!!!
Ahora vas y lo cascas!!!!!!!!