Comparación de binarios por grafo
Hace ya bastante tiempo me puse a mirar como buscar similitudes entre programas basándose exclusivamente en grafos y estadísticas de los mismos, procurando huir siempre que fuera posible del código ensamblador, con la ayuda de muchas ideas de la gente de 48bits, especialmente. La idea es poder buscar similitudes entre múltiples binarios para agruparlos (por ejemplo, para crear subgrupos de baterías de malware similares a partir de una batería más grande) o comparar 2 binarios y extraer sus similitudes (útil para buscar vulnerabilidades corregidas en parches, aunque este post no va de eso). El resultado de todo esto es una serie de algoritmos «WorksForMe» (TM) qué he implementado utilizando Pyew (inicialmente la idea era utilizar IDA pero, a pesar de que funcione mejor, me gusta más utilizar software libre y a poder ser mío, manías).
¿Qué coño es eso de Pyew?
Para quienes no lo conozcan, Pyew es un proyecto Open Source muy similar a radare o hiew, escrito en Python y principalmente orientado a la automatización de análisis de malware. Pyew tiene soporte para muchos formatos de archivo (PDF, OLE2, …) pero los que nos importan ahora son PEs y ELF (aunque el soporte de ELF no es muy bueno que se diga).
Análisis de código
Cuando abrimos un archivo de este tipo (PE o ELF) Pyew realiza análisis de código para encontrar las funciones que se encuentren en este binario. Utiliza un algoritmo muy similar al de IDA: Analiza, instrucción por instrucción, todos los puntos de entrada del binario y va buscando llamadas a funciones, poniéndolas en una cola para posterior análisis, hasta agotar todos los elementos de dicha cola (podéis leer más del algoritmo utilizado en Pyew aquí). Después de este paso, opcionalmente, se pondrá a buscar funciones buscando los prólogos de función más típicos de x86 y x86_64.
Una vez que el análisis ha finalizado, se realizan unos cálculos estadísticos, y se obtienen muchos datos interesantes para la agrupación o búsqueda de similitudes, siendo los más importantes los siguientes:
- Funciones.
- Bloques básicos.
- Datos estadísticos de cada función (grado de entrada, de salida y complejidad ciclomática).
- Datos estadísticos del programa (media, máxima y mínima del número de nodos, aristas y valores de complejidad ciclomática).
Explicado lo básico, vamos a ver los algoritmos que he implementado.
Algoritmo 1: Sistema experto
Esta fue una de las primeras ideas que tuve: Teniendo los datos de complejidad ciclomática media, máxima, mínima así como el número de funciones de un binario, esto se podría utilizar como un hash para comparar, rápidamente, 2 o varios binarios. Si todos los datos son iguales, los binarios son clasificados como «100% similares» (que no iguales). Si no lo son, entonces se calcula la distancia de estos valores y se le asigna un porcentaje a cada valor sacado:
- Media de la complejidad ciclomática: 50% de la diferencia.
- Máxima de la complejidad ciclomática: 30% de la diferencia.
- Mínima de la complejidad ciclomática: 10% de la diferencia.
- Total de funciones: 10% de la diferencia.
El siguiente es el código de ejemplo utilizado:
# This code is under the GPLv2
import os, sys
from hashlib import sha256
from pyew_core import CPyew
class CExpertCluster(object):
def __init__(self, data):
self.data = data
def compareTwoSets(self, set1, set2):
# Get the ciclomatic complexity statistical data of the 2 samples
ccs1 = set1.values()[0].program_stats["ccs"]
ccs2 = set2.values()[0].program_stats["ccs"]
avg_cc_distance = abs(ccs1["avg"] – ccs2["avg"])
max_cc_distance = abs(ccs1["max"] – ccs2["max"])
min_cc_distance = abs(ccs1["min"] – ccs2["min"])
total_functions = abs(len(set1.values()[0].functions) – len(set2.values()[0].functions))
difference = avg_cc_distance*0.5 + \
max_cc_distance*0.3 + \
min_cc_distance*0.1 + \
total_functions*0.1
return difference
def cluster(self):
set1 = self.data[0]
set2 = self.data[1]
return self.compareTwoSets(set1, set2)
class CGraphCluster(object):
def __init__(self):
self.clear()
self.deep = False
self.timeout = 0
def addFile(self, filename):
self.files.append(filename)
def clear(self):
self.files = []
self.results = []
self.data = []
def processFile(self, filename):
print "[+] Analyzing file %s" % filename
pyew = CPyew(batch=True)
pyew.deepcodeanalysis = self.deep
pyew.analysis_timeout = 0
pyew.loadFile(filename)
if pyew.format in ["PE", "ELF"]:
hash = sha256(pyew.getBuffer()).hexdigest()
self.data.append({hash:pyew})
else:
print "Not a PE/ELF file"
def compareExpert(self):
cluster = CExpertCluster(self.data)
val = cluster.cluster()
if val == 0:
print "Expert system: Programs are 100% equals"
else:
print "Expert system: Programs differs in %f%s" % (round(val, 1), "%")
return val
def processFiles(self):
for f in self.files:
self.processFile(f)
def main(prog1, prog2):
cluster = CGraphCluster()
cluster.addFile(prog1)
cluster.addFile(prog2)
cluster.processFiles()
cluster.compareExpert()
def usage():
print "Usage:", sys.argv[0], "file1 file2"
if __name__ == "__main__":
if len(sys.argv) != 3:
usage()
else:
main(sys.argv[1], sys.argv[2])
Y ahora explico un poco el código. Hay 2 clases:
- CGraphCluster: Es la clase principal, encargada de analizar los archivos pasados con pyew y guardar sus datos en miembros de la clase.
- CExpertCluster: Esta es la clase que se encarga realmente de comparar los 2 binarios, con el algoritmo comentado, a partir de los datos sacados con pyew.
Prueba
Para hacer las pruebas voy a coger primero unos cuantos programas de ejemplo muy simples, y compilarlos con Mingw en PEs: clean.c, test.c, test2.c, test3.c, test4.c y test5.c. Y ahora vamos a ver que tal se porta este sistema de comparaciones:
$ graph_test1.py clean.exe test.exe [+] Analyzing file clean.exe [+] Analyzing file test.exe Expert system: Programs differs in 0.100000% $ graph_test1.py clean.exe test2.exe [+] Analyzing file clean.exe [+] Analyzing file test2.exe Expert system: Programs differs in 0.900000% $ graph_test1.py clean.exe test3.exe [+] Analyzing file clean.exe [+] Analyzing file test3.exe Expert system: Programs differs in 0.900000% $ graph_test1.py clean.exe test4.exe [+] Analyzing file clean.exe [+] Analyzing file test4.exe Expert system: Programs differs in 1.000000% $ graph_test1.py clean.exe test5.exe [+] Analyzing file clean.exe [+] Analyzing file test5.exe Expert system: Programs differs in 1.000000%
Como se puede ver, parece que el sistema funciona medianamente bien con los programas de ejemplo. El siguiente paso es probarlo con malware. Para ese ejemplo he probado con los archivos siguientes:
e1acaf0572d7430106bd813df6640c2e HGWC.ex_ 73be87d0dbcc5ee9863143022ea62f51 BypassXtrap.ex_
Si probamos a comparar esto archivos con, por ejemplo, ssdeep, veremos que nos dice que no se parecen ni en el ano:
$ ssdeep -b HGWC.ex_ BypassXtrap.ex_ ssdeep,1.0--blocksize:hash:hash,filename 12288:faWzgMg7v3qnCiMErQohh0F4CCJ8lnyC8rm2NY:CaHMv6CorjqnyC8rm2NY,"HGWC.ex_" 49152:C1vqjdC8rRDMIEQAePhBi70tIZDMIEQAevrv5GZS/ZoE71LGc2eC6JI/Cfnc:C1vqj9fAxYmlfACr5GZAVETeDI/Cvc,"BypassXtrap.ex_"
Sin embargo, si hacemos la prueba con este script:
$ graph_test1.py HGWC.ex_ BypassXtrap.ex_ [+] Analyzing file HGWC.ex_ [+] Analyzing file BypassXtrap.ex_ Expert system: Programs are 100% equals
Un análisis un poco más en profundidad de los bitxos y tal muestra que ambos están empacados con AutoIt.
Problemas de este algoritmo
Uno de los problemas más claros de este algoritmo es que agrupando por grafo estaríamos agrupando por el packer, si los archivos no están desempacados, como está claro. Sin embargo, a veces, también interesa agrupar por packers (por ejemplo, por packers de malware).
Otro de los problemas es que es relativamente fácil crear colisiones: se podrían hacer binarios que generasen el mismo hash que, por ejemplo, el notepad de Windows, de un modo no demasiado complicado (poniendo funciones que no hagan nada más que cambiar los datos estadísticos).
Además, hay que tener en cuenta otro problema más: Solo vale para comparar 2 archivos, no para comparar grupos de archivos. Aunque siempre se podrían utilizar los datos en que se basa este algoritmo para realizar la agrupación (como se verá en la herramienta ya finalizada).
Algoritmo 2: Comparación con números primos y firma de funciones
En este caso lo que se hace es coger para cada función los datos de grado de entrada, grado de salida y complejidad ciclomática (una lista [indegree, outdegree, complexity]) y considerar estos 3 datos como la firma de la función (es decir, una función con firma [1, 2, 3] en un binario se considera que es igual a otra función con esa misma firma en otro binario).
Además de obtenerse este conjunto para cada binario, con la complejidad ciclomática de cada función, se obtiene un número primo asociado a su valor y se multiplican todos los valores encontrados excluyendo repetidos. Es decir, si una función tiene complejidad 5, se coge el 5º primo, si la siguiente función tiene complejidad 19, se coge el 19º primo y, suponiendo que un binario solo tuviera estas 2 funciones, el hash rápido generado basado en números primos será la multiplicación del 5º primo * 19º primo. De esta multiplicación, se excluyen aquellas funciones cuya complejidad ciclomática sea 1.
Una vez que se tienen calculados ambos datos (los grupos de firmas de función de cada binario y el hash hecho con números primos) se compara primero el hash, si este es igual, se considera que el binario es «100% similar» (repito, que no igual) y ya no es necesario continuar haciendo nada más. En caso de que no coincida el hash, se obtiene el total de elementos de la intersección de ambos conjuntos (estamos suponiendo la comparación de 2 binarios), el total de elementos de la diferencia de conjuntos y el número máximo de elementos de conjuntos (es decir, el mayor del total de elementos del conjunto 1 y conjunto 2). Y, finalmente, con estos datos se procede al cálculo de la diferencia entre ambos binarios.
Menuda mierda de explicación
Ya, no se entiende una oxtia, intentaré explicarme mejor respondiendo a las preguntas típicas acerca de este algoritmo:
- ¿Para qué generas un valor con números primos si luego, en caso de que no coincidan, realizas unas operaciones donde nada tienen que ver los números primos? El valor obtenido multiplicando los números primos se utiliza para hacer una comprobación rápida de 2 o más archivos, es decir, si estoy comparando 100 archivos a la vez, mirar si el valor obtenido es igual es más rápido que comprobar la intersección y diferencia de conjuntos.
- ¿Cómo se aplica esto para varios archivos? Hoy por hoy, lo hago comparando cada archivo con todos los demás. Es decir, si tengo 100 archivos, haré 100*100 comparaciones.
Prueba
Para probar este algoritmo, agregamos el siguiente código al archivo graph_test1.py anterior:
if n==2: return [2]
elif n<2: return []
s=range(3,n+1,2)
mroot = n ** 0.5
half=(n+1)/2-1
i=0
m=3
while m <= mroot:
if s[i]:
j=(m*m-3)/2
s[j]=0
while j<half:
s[j]=0
j+=m
i=i+1
m=2*i+3
return [2]+[x for x in s if x]
class CPrimesCluster(object):
def __init__(self, data):
self.primes = primes(1024*1024)
self.data = data
def generateHash(self, pyew):
val = 1.
dones = []
primes_done = []
for f in pyew.functions:
nodes, edges, cc = pyew.function_stats[f]
if cc > 1 and (nodes, edges, cc) not in dones:
p = self.primes[cc]
if p not in primes_done:
val *= p
primes_done.append(p)
dones.append((nodes, edges, cc))
return val, dones
def compareManySets(self, sets):
files = {}
primes = {}
values = {}
print "File1;File2;Difference"
for s in sets:
pyew = s.values()[0]
val, prime = self.generateHash(pyew)
hash = sha256(pyew.getBuffer()).hexdigest()
primes[hash] = prime
values[hash] = val
files[hash] = pyew.filename
del pyew
dones = []
size = len(primes)
for h1 in values:
for h2 in values:
if h1 == h2 or (h1, h2) in dones or (h2, h1) in dones:
continue
if values[h1] == values[h2]:
print "%s;%s;0" % (files[h1], files[h2])
dones.append((h1, h2))
dones.append((h2, h1))
else:
dones.append((h1, h2))
dones.append((h2, h1))
s1 = set(primes[h1])
s2 = set(primes[h2])
diff = self.getSimilarity(s1, s2)
print "%s;%s;%f" % (files[h1], files[h2], diff)
def getSimilarity(self, s1, s2):
m = max(len(s1), len(s2))
diff1 = len(s1.difference(s2))
diff2 = len(s2.difference(s1))
diff = (diff1 + diff2)*100./m
simil1 = len(s1.intersection(s2))
simil = simil1*100. / m
metric = simil + diff
diff = diff * 100. / metric
return diff
def compareTwoSets(self, set1, set2):
pyew1 = set1.values()[0]
val1, primes1 = self.generateHash(pyew1)
pyew2 = set2.values()[0]
val2, primes2 = self.generateHash(pyew2)
s1 = set(primes1)
s2 = set(primes2)
if val1 == val2:
return 0
else:
diff = self.getSimilarity(s1, s2)
return diff
def cluster(self):
if len(self.data) == 2:
set1 = self.data[0]
set2 = self.data[1]
return self.compareTwoSets(set1, set2)
else:
return self.compareManySets(self.data)
Luego en la clase CGraphCluster agregamos el siguiente método:
cluster = CPrimesCluster(self.data)
val = cluster.cluster()
if val == 0:
print "Primes system: Programs are 100% equals"
else:
print "Primes system: Programs differs in", val, "% percent"
Y, finalmente, cambiamos la función main para que quede como sigue:
cluster = CGraphCluster()
cluster.addFile(prog1)
cluster.addFile(prog2)
cluster.processFiles()
cluster.compareExpert()
cluster.comparePrimes()
Una vez hechos los cambios empezamos a probar el algoritmo con los mismos ejemplos anteriores (los programitas tontos de antes y los 2 ejemplos de malware). Los resultados son los siguientes:
$ graph_test1.py clean.exe test.exe [+] Analyzing file clean.exe [+] Analyzing file test.exe Expert system: Programs differs in 0.100000% Primes system: Programs differs in 14.2857142857 % percent $ graph_test1.py clean.exe test2.exe [+] Analyzing file clean.exe [+] Analyzing file test2.exe Expert system: Programs differs in 0.900000% Primes system: Programs differs in 25.0 % percent $ graph_test1.py clean.exe test3.exe [+] Analyzing file clean.exe [+] Analyzing file test3.exe Expert system: Programs differs in 0.900000% Primes system: Programs differs in 25.0 % percent $ graph_test1.py clean.exe test4.exe [+] Analyzing file clean.exe [+] Analyzing file test4.exe Expert system: Programs differs in 1.000000% Primes system: Programs differs in 37.5 % percent $ graph_test1.py clean.exe test5.exe [+] Analyzing file clean.exe [+] Analyzing file test5.exe Expert system: Programs differs in 1.000000% Primes system: Programs differs in 25.0 % percent $ graph_test1.py HGWC.ex_ BypassXtrap.ex_ [+] Analyzing file HGWC.ex_ [+] Analyzing file BypassXtrap.ex_ Expert system: Programs are 100% equals Prime: Programs are 100% equals
Como se puede ver este sistema ‘funciona’, aunque da porcentajes muy diferentes con los ejemplos de prueba anteriores. Con los 2 bitxos empacados con AutoIt, sin embargo, nos sigue diciendo que son exactamente iguales.
Problemas
Los problemas de este algoritmo son exactamente los mismos que en el caso anterior: Agrupa por packer y se podría (aunque con este algoritmo se hace más complicado) hacer un programa que tuviera la misma firma que un notepad y diferente comportamiento (un malware, por ejemplo).
Herramienta final
El script ya finalizado con algunas cositas más lo podéis descargar aquí (requiere Pyew, acordaros). Las modificaciones que tiene este script son para utilizarlo con baterías de archivos. Puede recibir 2 parámetros, siendo 2 programas (ELF o PE) a comparar o un directorio. En caso de ser un directorio, se analizan todos los archivos de ese directorio y sus subdirectorios y se imprime, con formato CSV, la lista de archivos, hashes y todos los datos obtenidos de las funciones.
Uso de la herramienta con baterías
El archivo CSV generado se puede utilizar con GNumeric, LibreOffice/OpenOffice o MS Office para ver que grupos existen (o importarlo a una base de datos). Voy a mostrar una prueba con una batería de 28 malwares (detectados por varios AVs como TDSS.Z, aunque realmente hay un poco de todo). Los siguientes son los resultados con la herramienta ssdeep:
En esta imagen se puede ver que la herramienta, por fuzzy hashing, solo encuentra 2 archivos similares. En la siguiente imagen se muestran los resultados con deeptoad:
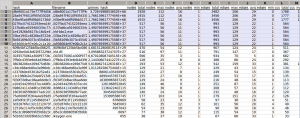
Vemos que esta herramienta consigue encontrar alguna similitud más agrupando 4 archivos. Ahora hagamos la prueba con los datos que genera la herramienta de comparación por grafos:
Y en este caso vemos que se crea un grupo más grande. Si comparamos los 10 archivos que ha agrupado veremos que en la mayoría de casos nos dirá que son 100% similares y, en otros, que las diferencias entre ellos son mínimas, como por ejemplo con los 2 primeros archivos que se ven en la imagen:
$ gcluster.py d8e8001a175e777ff4d56a6a7b9d32f37178cc24010d4e4d0e8e4027ac69c54d 28a847f4010f95fd3302816559b8cc4be433445aad26b04ff3d688e42ae5b0a1 Expert system: Programs differs in 0.100000% Primes system: Programs differs in 16.8421052632 % percent
Notas finales
De momento lo dejo aquí porque el post ya es bastante grande. Seguramente vuelva a postear algo más acerca de grafos en el futuro pero, de momento, aquí se acaba. Espero que os haya gustado este totxazo de post y que os pueda valer para algo.
Muchas gracias a toda la peña de 48bits por su ayuda y especialmente a Marconi por haberme ayudado con correcciones a los algoritmos y con el post.