Desde hace algunas semanas El Pais esta publicando unos retos matematicos semanales, y entre los acertantes de cada desafio se sortea la coleccion completa de libros de matematicas que el periodico esta vendiendo cada domingo. Desde mi punto de vista el acierto de estos desafios es la eleccion de problemas que son entretenidos y asequibles para el gran publico. Como ejemplo podemos analizar el problema de la semana pasada. Podeis ver el video del desafio aqui.

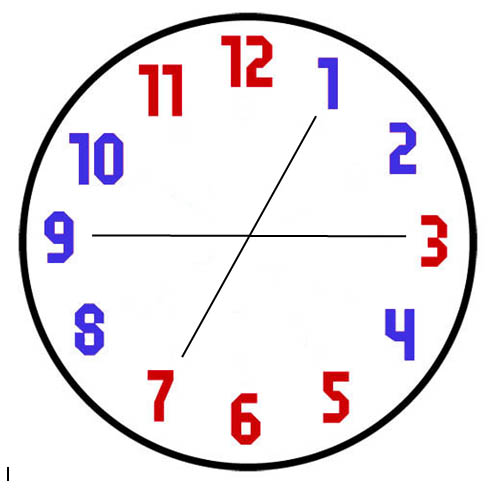
Comencemos poniendo una esfera ejemplo con sus numeros coloreados de azul y rojo. Tened en cuenta que esta esfera sirve solo como ejemplo, y que nosotros debemos demostrar que nuestro sistema funciona para cualquier esfera, incluida esta.

Si analizamos el problema proupesto, vemos que no se trata de un problema dificil. A continuacion voy a exponer una posible solucion. Tenemos que demostrar que siempre se puede dibujar una linea que corte al reloj en dos y que deje tres numeros rojos y tres numeros azules a cada lado. Nosotros vamos a demostrar que esto es asi, y ademas vamos a proponer un mecanismo que nos permitira saber cuantas soluciones existen y cuales son.

Vamos a comenzar imaginandonos que dibujamos una linea uniendo cada uno de los numeros de la esfera del reloj con el numero que tiene en frente. Todas estas lineas, seis en total, se cruzaran en el centro.

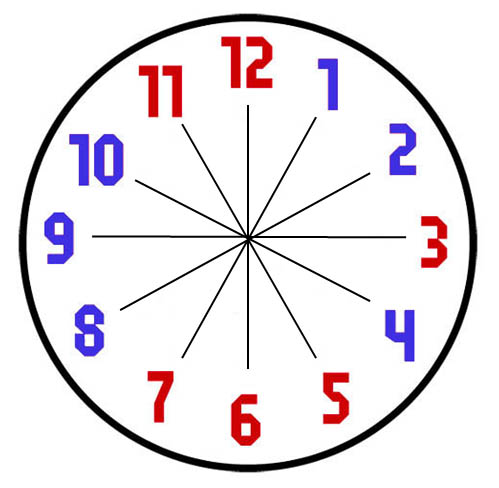
El primer dato que hemos de tener en cuenta es que para cada una de estas parejas, (12,6),(1,7),(2,8), etc. los dos numeros de la pareja no pueden pertenecer al mismo lado de la solucion. Esto es asi porque todas las lineas que hemos dibujado se cruzan en el centro, y la linea solucion se cruzara con todas ellas tambien en el centro del reloj, dejando siempre un numero de la pareja a un lado, y el segundo al otro.
Ahora, imaginemos que para todas estas parejas, ambos numeros tienen el mismo color. Entonces, cualquiera de las rectas que cruzando por el centro de la esfera divide el reloj en dos partes con seis numeros cada una, es una solucion del problema. Esto debe ser asi porque si para cada pareja un numero esta en un lado de la solucion y el otro esta en el otro lado de la solucion, y todas las parejas tiene los dos numeros del mismo color, entonces tenemos que encontrar necesariamente el mismo numero de digitos de cada color a ambos lados de cualquier recta que divide al realoj en dos.
De todo esto deducimos una cosa importante. Podemos ignorar las parejas que tienen los dos numeros del mismo color. Dibujemos nuestro reloj, dejando solo las rectas que representan parejas con numeros de diferentes colores:

Ahora, pasaremos a demostrar otro detalle que es importante para llegar a la solución final. El numero de parejas con numeros de diferentes colores es siempre un numero par. Lo podemos demostrar facilmente por reduccion al absurdo. Imaginemos que existe un numero impar de parejas con numeros de diferentes color, y sea este numero k, e imaginemos que para uno de los dos colores, por ejemplo el rojo, existen n parejas con los dos numeros de colo rojo. Entonces, la cantidad de numeros rojos en la esfera debe ser: 2*n+k. Como k es impar, ese numero es impar, pero la cantidad de numeros rojos y azules en la esfera es par : 6. Por lo tanto es imposible que haya un numero impar de parejas con numeros de diferente color.

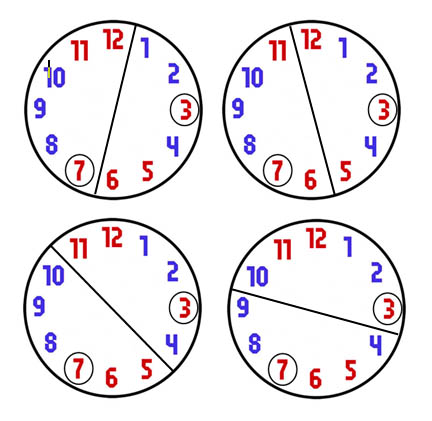
Ahora ya tenemos todas las piezas del puzzle. Las parejas con ambos numeros de igual color no crean desequilibrio entre las dos partes de la solucion y siempre hay un numero par de parejas con numeros de diferente color. Si elegimos un color, por ejemplo el rojo, y nos fijamos donde estan los numeros de cojor rojo de las parejas con numeros de diferente color, siempre podemos encontrar uno o varios puntos en el que dejamos la misma cantidad de numeros rojos a un lado y otro. La paridad de parejas nos garantiza la existencia de este punto. De esta forma garantizamos que la cantidad de numeros de color rojo, y por ende de color azul, a ambos lados de la solucion coinciden. Pero ademas de demostrar que siempre hay solucion, y de haber encontrado una, tambien hemos diseñado un mecanismo que nos permite saber cuantas soluciones hay y cuales son. Para el ejemplo con el que hemos empezado, existen varias soluciones. He marcado con un circulo los numeros que limitan la zona donde encontramos soluciones.

Como podeis ver, los problemas son asequibles y entretenidos. Asi que os animo a seguir estos retos matematicos. El de esta semana es mas sencillo que el de la semana pasada ;o)
Por cierto, si quereis ver otras soluciones, El Pais ha publicando algunas de ellas aqui.